TIL
20210116(토) : DP, Stack 본문
Stack : 10799
DP : 9095
DP
1 2 3 더하기
문제
https://www.acmicpc.net/problem/9095
정수 4를 1, 2, 3의 합으로 나타내는 방법은 총 7가지가 있다. 합을 나타낼 때는 수를 1개 이상 사용해야 한다.
- 1+1+1+1
- 1+1+2
- 1+2+1
- 2+1+1
- 2+2
- 1+3
- 3+1
정수 n이 주어졌을 때, n을 1, 2, 3의 합으로 나타내는 방법의 수를 구하는 프로그램을 작성하시오.
문제 풀이 과정
정수 n을 1, 2, 3의 합으로 나타낼 수 있는 경우의 수를 f(n)이라고 정의한다.
f(1) = 1, (1 하나밖에 없으므로)
f(2) = 2, { ( 2 ), (1 + 1) }
f(3) = 4, { ( 3 ), (1 + 2), (2 + 1), (1 + 1 + 1) }
....
....
f(7) 을 문제를 풀기 위한 예로 들겠다.
f(7) 을 만들기 위해서,
f(7) = 1 + f(6)
2 + f(5)
**3 + f(4)**f(7)을 1과 6을 더하는 경우, 2와 5를 더하는 경우, 3과 4로 더하는 경우의 수를 고려해봐야 한다.
즉, 7을 1,2, 그리고 3의 합으로 표현하고 싶다면
1에다가 6을 1,2,3의 합 으로 표현할 수 있는 경우를 더하여 고려한다.
1 + (4 + 1 + 1), 1 + (4 + 2) ,1 + (3 + 1 + 1 + 1), 1 + (3+ 2 + 1), 1 + (3 + 1 + 2)
...
2 + (4 + 1), 2 + (1 + 4), 2 + (3 + 1 + 1), 2 + (3 + 2), ...
....
3 + (4 ) , ...
1에 가능한 f(6) (1,2,3 의 합으로 6을 만들 수 있는 경우의 수)을 더하는 경우의 수를 모두 고려한 뒤
(1은 같은 위치에 고정적으로 더해주므로 f(6)만 고려해준다.)
같은 방법으로
2 에 가능한 f(5)를 더하는 순열을 고려하며,
같은 방법으로 3에 f(4)를 더하는 순열을 고려한다.
따라서 f(7) = f(6) + f(5) + f(4)의 식이 도출되면서
f(n) = f(n-1) + f(n-2) + f(n-3)의 점화식을 도출할 수 있다.
#include <iostream>
using namespace std;
int main()
{
int dp[12];
int t;
int n;
dp[0] = 1; dp[1] = 1; dp[2] = 2; dp[3] = 4;
cin >> t;
while (t--)
{
cin >> n;
for(int i = 4; i <= n; i++)
dp[i] = dp[i-1] + dp[i-2] + dp[i-3];
cout << dp[n] << endl;
}
}스택
쇠막대기
문제
https://www.acmicpc.net/problem/10799
여러 개의 쇠막대기를 레이저로 절단하려고 한다. 효율적인 작업을 위해서 쇠막대기를 아래에서 위로 겹쳐 놓고, 레이저를 위에서 수직으로 발사하여 쇠막대기들을 자른다. 쇠막대기와 레이저의 배치는 다음 조건을 만족한다.
- 쇠막대기는 자신보다 긴 쇠막대기 위에만 놓일 수 있다. - 쇠막대기를 다른 쇠막대기 위에 놓는 경우 완전히 포함되도록 놓되, 끝점은 겹치지 않도록 놓는다.
- 각 쇠막대기를 자르는 레이저는 적어도 하나 존재한다.
- 레이저는 어떤 쇠막대기의 양 끝점과도 겹치지 않는다.
아래 그림은 위 조건을 만족하는 예를 보여준다. 수평으로 그려진 굵은 실선은 쇠막대기이고, 점은 레이저의 위치, 수직으로 그려진 점선 화살표는 레이저의 발사 방향이다.
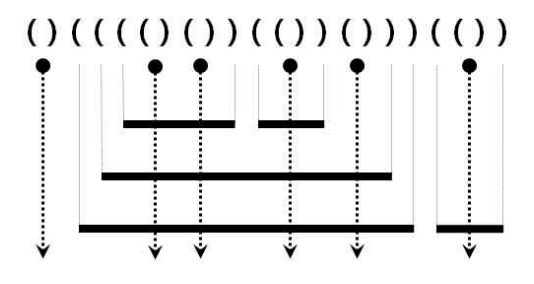
이러한 레이저와 쇠막대기의 배치는 다음과 같이 괄호를 이용하여 왼쪽부터 순서대로 표현할 수 있다.
- 레이저는 여는 괄호와 닫는 괄호의 인접한 쌍 ‘( ) ’ 으로 표현된다. 또한, 모든 ‘( ) ’는 반드시 레이저를 표현한다.
- 쇠막대기의 왼쪽 끝은 여는 괄호 ‘ ( ’ 로, 오른쪽 끝은 닫힌 괄호 ‘) ’ 로 표현된다.
위 예의 괄호 표현은 그림 위에 주어져 있다.
쇠막대기는 레이저에 의해 몇 개의 조각으로 잘려지는데, 위 예에서 가장 위에 있는 두 개의 쇠막대기는 각각 3개와 2개의 조각으로 잘려지고, 이와 같은 방식으로 주어진 쇠막대기들은 총 17개의 조각으로 잘려진다.
쇠막대기와 레이저의 배치를 나타내는 괄호 표현이 주어졌을 때, 잘려진 쇠막대기 조각의 총 개수를 구하는 프로그램을 작성하시오.
문제 풀이
- 열린 괄호가 등장하였다면, 뒤에 나오는 괄호가 닫힌 괄호인지 열린 괄호인지에 따라 레이저인지, 막대기인지가 결정된다.
- 만약, 열린 괄호 뒤 닫힌 괄호가 온다면 ()는 레이저다.
- 만약, 열린 괄호 뒤 열린 괄호가 온다면 (( 에서 ( 는 새로운 막대기의 시작을 알린다.
- 괄호가 닫히면서 레이저가 만들어지지 않는다면, 막대기의 끝을 알린다.
따라서, 문자열을 순서대로 훑으면서, 괄호에 따라 의미를 생각하면서 문제를 푼다.
() (((() ())(())( )))(( ))
를 예로 들어보자.
()는 레이저이고, 이전에 막대기가 존재하지 않았기 때문에, 막대기의 수는 0이다.
(((()에서 막대기 3개가 들어왔으며, 관통하는 레이저는 ()로, 1개다.
따라서, 막대기 3개가 생기는 것은 기정사실이다.
그 뒤로 ()가 하나 더 존재하며, 다시 잘린막대기 3개가 더 생긴다.
그 뒤로 )가 오면서, 막대기 하나의 길이의 끝을 알린다.
막대기 길이의 끝에서는 잘린 막대기가 하나 생긴다.
따라서, 막대기는 2개가 되었다.
그 뒤로, (())가 오면서, 막대기는 다시 2 + 1개가 되고, 레이저가 막대기 2 + 1개를 자르면서 잘린막대기 3개가 더 생기면서, 닫힌 괄호로 막대기 1개 길이의 끝을 알린다.
그 뒤는 생략한다.
위를 표현한 코드이다.
#include <iostream>
#include <string>
using namespace std;
int main()
{
int numstick;
int sum;
char c;
string input;
int i;
getline(cin, input);
i = numstick = sum = 0;
do
{
if (input[i] == '(')
numstick++;
else
{
if (input[i - 1]== '(')
{
numstick--;
sum += numstick;
}
else
{
sum += 1;
numstick--;
}
}
} while (input[++i] != '\0') ;
cout << sum;
return (0);
}
아래는 스택을 사용해서 만든 코드다.
달라진 점이라면, 현재 막대기의 개수를 나타내는 변수는 스택을 사용한 코드에서는 존재하지 않고
스택의 element의 개수로 표현되었다.
#include <stack>
#include <iostream>
#include <string>
using namespace std;
int main()
{
string input;
int stick_num;
int sum;
stack<int> stk;
getline(cin, input);
stick_num = sum = 0;
for(int i = 0; input[i] != '\0'; i++)
{
if (input[i] == '(')
stk.push(1);
else
{
stk.pop();
if (input[i - 1] == '(')
{
sum += stk.size();
}
else
sum += 1;
}
}
cout << sum;
}
'2021 > 일일 기록' 카테고리의 다른 글
| 20210203 집단 넋두리 (0) | 2021.02.04 |
|---|---|
| 20210201(월) - printf (0) | 2021.02.02 |
| 20210115(금) :get_line() (0) | 2021.01.16 |
| 20210106(수) 넷 (0) | 2021.01.06 |
| 20210105(화) (0) | 2021.01.05 |

